통계 분석의 본질은 측정에 내재된 불확실성을 탐색하는 것입니다.
예를 들어, 우리나라 기업의 평균 매출액을 계산해야 한다고 가정해 보죠. 우리나라의 모든 기업의 매출금액을 확인하여 평균을 낸다는 것은 현실적으로 너무 어렵습니다. 불가능에 가깝죠. 그래서 임의로 50개 기업을 선정하여 해당 기업의 평균 매출금액을 산출하여, 이 수치가 우리나라 전체 기업의 평균 매출액이라고 결론을 내렸습니다.
이 수치가 전체 우리나라 기업의 평균 매출액을 정확하게 반영했다고 할 수 있을까요? 이런 상황에서 나오는 개념이 신뢰구간입니다. 신뢰구간의 의미는 실제 평균이나 다른 모수를 포함할 가능성이 있는 범위를 정의하여 이러한 불확실성을 어느 정도 해결합니다.
신뢰구간 의미
신뢰구간은 평균이나 비율과 같이 우리가 알고자 하는 특정 값(모수)를 포함할 것으로 예상되는 값의 범위입니다.
통계학에서는 95%의 의 신뢰구간과 99%의 신뢰구간을 많이 사용합니다. 95% 신뢰구간의 의미는 우리가 데이터 추출을 통해서 100번의 신뢰구간을 산출할 경우, 그 중 95번 정도는 우리가 알고자 하는 특정 값(모수)가 우리가 예상하는 값의 범위에 포함된다는 의미입니다.
중심극한정리 (CLT)
중심극한정리는 표본 평균은 표본 크기가 커짐에 따라 모집단의 분포와 관계없이 정규 분포를 따르게 된다는 이론입니다. 이 정리는 표본 크기가 충분히 크다고 가정할 때(일반적으로 30 이상) 다양한 데이터 분포에 정규 분포를 고려한 신뢰 구간을 적용할 수 있게 해줍니다.
중심극한정리 예시
우리나라 모든 기업의 평균 매출금액을 알고 싶습니다. 모든 기업을 조사하는 것은 비현실적입니다. 대신 무작위로 표본을 추출하기로 결정했습니다.
모집단 데이터(간소화) :
- 우리나라 기업의 매출은 매우 다양합니다.
- 대기업부터 소상공인까지 매출액의 분포가 매우 다양합니다.
접근 방안:
- 다양한 샘플 데이터 수집: 무작위로 40개(샘플) 기업을 선택하여 매출액을 기록합니다. 이를 30번 반복하여 30개의 다른 샘플 데이터를 생성합니다.
- 샘플 평균 계산: 각 샘플 기업에 대해 평균 매출금액을 계산합니다.
5개 샘플의 결과:
- 샘플 1: 평균 매출금액 = 35억
- 샘플 2: 평균 매출금액 = 38억
- 샘플 3: 평균 매출금액 = 42억
- 샘플 4: 평균 매출금액 = 37억
- 샘플 5: 평균 매출금액 = 40억
위의 과정을 계속하면서, 각 샘플의 평균 매출금액 중심극한정리에 의해 정규 분포와 비슷해지기 시작하는 분포를 형성한다는 것을 관찰할 수 있습니다. 이는 원래 기업의 연령 매출금액이 정규 분포가 아니었음에도 불구하고 나타나는 결과입니다.
중심극한정리를 신뢰 구간에 연결
중심극한정리는 모집단 분포에 관계없이 표본 평균의 분포는 표본 크기가 충분히 커질 때(일반적으로 30개 이상의 표본으로 간주됨) 정규 분포에 근접한다고 말합니다.
이는 모집단 데이터가 정규 분포를 따르지 않더라도 신뢰구간과 같이 정규성을 가정하는 통계 기법을 적용할 수 있기 때문에 매우 중요합니다.
실제적 의미:
모집단에서 표본을 추출하고 해당 표본의 평균을 계산한 다음 중심극한정리를 사용하여 해당 평균 주변에 신뢰 구간을 적용하는 것이 가능합니다. 이 신뢰 구간은 특정 수준의 신뢰(예: 95%)로 실제 모집단 평균이 어디에 있는지 추정할 수 있습니다.
중심극한정리를 이용한 신뢰 구간의 실제 사례
도시 성인의 평균 신장을 추정하는 데 관심이 있다고 가정해 보겠습니다. 모든 개인을 측정할 수 없으므로 무작위 표본을 추출합니다. 표본이 100명의 성인으로 구성되어 있다고 가정하고, 이 표본에서 구한 신장의 평균은 170cm, 표준 편차는 10cm입니다.
1단계: 표본 평균 계산
표본 평균(x̄)은 표본의 평균 키인 170cm입니다.
2단계: 신뢰 수준 및 해당 Z-점수 결정
구간에 대한 신뢰 수준을 선택합니다. 일반적으로 95% 신뢰 수준이 사용되며, 이는 Z-Score 1.96에 해당합니다. 이 Z-Score는 표준 정규 분포에서 나오며 꼬리(각각 곡선 아래 데이터의 2.5%를 나타냄)가 평균에서 1.96 표준 편차 떨어져 있음을 나타냅니다.
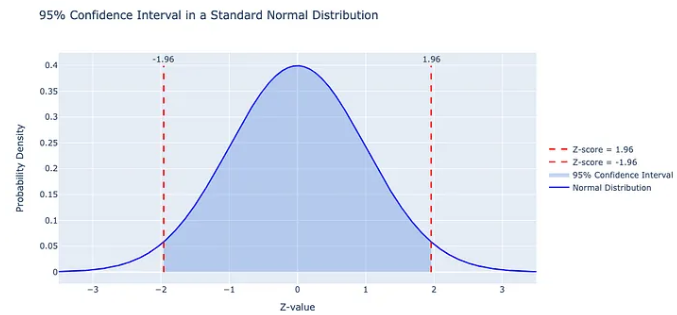
3단계: 표준 오차 계산
표준 오차(E)는 다음 공식을 사용하여 계산합니다.
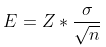
- Z는 우리가 선택한 신뢰 수준(95%의 경우 1.96)에 해당하는 Z- Score입니다.
- σ는 샘플의 표준 편차(10cm)입니다.
- n은 샘플 크기(100)입니다.
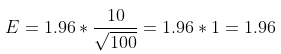
4단계: 신뢰 구간 구성
신뢰 구간은 표본 평균을 중심으로 구성되며, 양쪽의 오차 한계를 확장합니다.
구간 = x̄±E
구간 = 170 ± 1.96
따라서 평균 키의 95% 신뢰 구간은 168.04cm와 171.96cm 사이입니다.
5단계: 해석
평균 신장에 대한 신뢰 구간(168.04cm~171.96cm)의 해석을 잘해야 합니다. 그것은 단순히 도시의 성인 평균 신장이 168.04cm~171.96cm 사이에 포함될 확률이 95%라고 말하는 것이 아닙니다. 이 수치는 1번의 샘플 과정을 통해서 생성된 신뢰구간입니다.
100개의 샘플을 다시 추출하여 계산하면, 신뢰구간은 달라지게 됩니다. 1번, 2번, 3번,… 100번 반복하면, 총 100개의 신뢰구간을 구할 수 있습니다. 실제 평균 신장은 100개의 신뢰구간 중에 95개에 포함될 가능성이 있다는 뜻으로 해석해야 합니다.
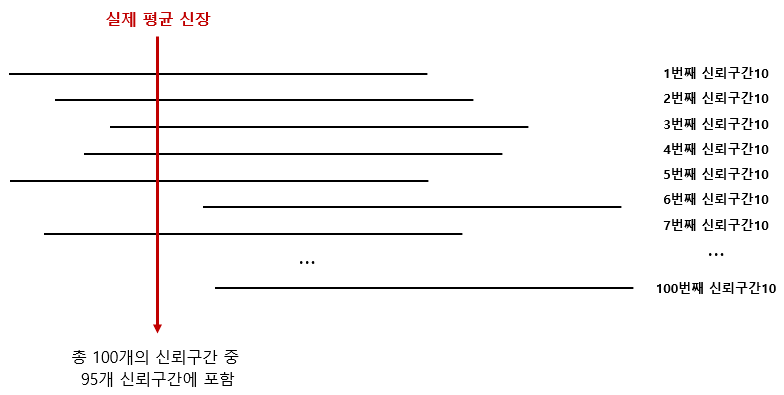
신뢰구간 설명을 위한 파이썬 구현
다음은 z-Score가 1.96인 신뢰 구간을 계산하기 위한 파이썬 구현입니다.
import numpy as np
def confidence_interval(data, z_score=1.96):
# 평균 및 표준편차 계산
mean = np.mean(data)
std_dev = np.std(data)
# 신뢰구간 상/하한 값 계산
lower_bound = mean - (z_score * std_dev)
upper_bound = mean + (z_score * std_dev)
return lower_bound, upper_bound
# 사용 예시
data = np.random.normal(loc = 50, scale = 10, size = 100) # 평균이 50이고, 표준편차가 10인 샘플 데이터
lower_bound, upper_bound = confidence_interval(data)
print(f"Confidence Interval (95%): [{lower_bound:.2f}, {upper_bound:.2f}]")
-------------------------------------------------------------------------------------------------------------------
Confidence Interval (95%): [29.38, 68.77]결론
신뢰구간은 통계학에서 데이터 분석의 불확실성을 이해하는 방법을 제공하는 기본 도구입니다. 진정한 가치가 있다고 믿는 범위를 제공함으로써 완전한 정보가 없더라도 정보에 입각한 결정을 내릴 수 있게 해줍니다.
실제 사례를 통해 신뢰구간을 어떻게 구성하고 적용하는지 살펴보았습니다. 다양한 분야에서 신뢰 구간의 중요성을 강조했습니다. 프로젝트에 뛰어들 때 신뢰 구간의 중요성을 잊지 마시기 바랍니다.
신뢰 구간은 숫자에 관한 것이 아니라 정확하고 실용적인 방식으로 데이터를 이해하는 것입니다.