신용카드 거래에서 사기를 탐지하는 것은 머신러닝의 중요한 응용 분야 중 하나 입니다. 이번 포스팅에서는 Kaggle의 신용카드 사기 거래 탐지 데이터 세트를 활용하여 신용카드 사기 거래 탐지 예측 모델 개발에 접근하는 방법에 대해서 알아 보겠습니다.
데이터 출처: 신용카드 사기 거래 탐지 데이터세트
https://www.kaggle.com/mlg-ulb/creditcardfraud
1단계: 데이터 전처리
필요한 라이브러리를 가져오고 데이터 세트를 Pandas DataFrame에 로드해야 합니다.
# 필요한 라이브러리 가져오기
import pandas as pd
# 데이터를 Pandas 데이터프레임으로 로드하기
# 데이터를 D드라이브에 저장한 경우의 로드 방법
creditcardData = pd.read_csv('D:/creditcard.csv')
# 데이터 탐색
creditcardData.head()
---------------------------------------------------------------
Time V1 V2 V3 V4 V5 V6 V7 \
0 0.0 -1.359807 -0.072781 2.536347 1.378155 -0.338321 0.462388 0.239599
1 0.0 1.191857 0.266151 0.166480 0.448154 0.060018 -0.082361 -0.078803
2 1.0 -1.358354 -1.340163 1.773209 0.379780 -0.503198 1.800499 0.791461
3 1.0 -0.966272 -0.185226 1.792993 -0.863291 -0.010309 1.247203 0.237609
4 2.0 -1.158233 0.877737 1.548718 0.403034 -0.407193 0.095921 0.592941
V8 V9 ... V21 V22 V23 V24 V25 \
0 0.098698 0.363787 ... -0.018307 0.277838 -0.110474 0.066928 0.128539
1 0.085102 -0.255425 ... -0.225775 -0.638672 0.101288 -0.339846 0.167170
2 0.247676 -1.514654 ... 0.247998 0.771679 0.909412 -0.689281 -0.327642
3 0.377436 -1.387024 ... -0.108300 0.005274 -0.190321 -1.175575 0.647376
4 -0.270533 0.817739 ... -0.009431 0.798278 -0.137458 0.141267 -0.206010
V26 V27 V28 Amount Class
0 -0.189115 0.133558 -0.021053 149.62 0
1 0.125895 -0.008983 0.014724 2.69 0
2 -0.139097 -0.055353 -0.059752 378.66 0
3 -0.221929 0.062723 0.061458 123.50 0
4 0.502292 0.219422 0.215153 69.99 0
[5 rows x 31 columns]2단계: 데이터 탐색
데이터세트의 구조, 요약 통계, class 분포(사기성 신용카드거래와 비사기성 신용카드거래)를 확인하여 데이터세트를 이해합니다.
# 데이터 세트의 행과 열의 갯수 확인
creditcardData.shape
--------------------------------------
(284807, 31)데이터 세트는 284,807개의 행과 31개의 열로 구성되어 있습니다.
# 요약 통계량 확인
print(creditcardData.describe())
--------------------------------------
Time V1 V2 V3 V4 \
count 284807.000000 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean 94813.859575 1.168375e-15 3.416908e-16 -1.379537e-15 2.074095e-15
std 47488.145955 1.958696e+00 1.651309e+00 1.516255e+00 1.415869e+00
min 0.000000 -5.640751e+01 -7.271573e+01 -4.832559e+01 -5.683171e+00
25% 54201.500000 -9.203734e-01 -5.985499e-01 -8.903648e-01 -8.486401e-01
50% 84692.000000 1.810880e-02 6.548556e-02 1.798463e-01 -1.984653e-02
75% 139320.500000 1.315642e+00 8.037239e-01 1.027196e+00 7.433413e-01
max 172792.000000 2.454930e+00 2.205773e+01 9.382558e+00 1.687534e+01
V5 V6 V7 V8 V9 \
count 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean 9.604066e-16 1.487313e-15 -5.556467e-16 1.213481e-16 -2.406331e-15
std 1.380247e+00 1.332271e+00 1.237094e+00 1.194353e+00 1.098632e+00
min -1.137433e+02 -2.616051e+01 -4.355724e+01 -7.321672e+01 -1.343407e+01
25% -6.915971e-01 -7.682956e-01 -5.540759e-01 -2.086297e-01 -6.430976e-01
50% -5.433583e-02 -2.741871e-01 4.010308e-02 2.235804e-02 -5.142873e-02
75% 6.119264e-01 3.985649e-01 5.704361e-01 3.273459e-01 5.971390e-01
max 3.480167e+01 7.330163e+01 1.205895e+02 2.000721e+01 1.559499e+01
... V21 V22 V23 V24 \
count ... 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean ... 1.654067e-16 -3.568593e-16 2.578648e-16 4.473266e-15
std ... 7.345240e-01 7.257016e-01 6.244603e-01 6.056471e-01
min ... -3.483038e+01 -1.093314e+01 -4.480774e+01 -2.836627e+00
25% ... -2.283949e-01 -5.423504e-01 -1.618463e-01 -3.545861e-01
50% ... -2.945017e-02 6.781943e-03 -1.119293e-02 4.097606e-02
75% ... 1.863772e-01 5.285536e-01 1.476421e-01 4.395266e-01
max ... 2.720284e+01 1.050309e+01 2.252841e+01 4.584549e+00
V25 V26 V27 V28 Amount \
count 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05 284807.000000
mean 5.340915e-16 1.683437e-15 -3.660091e-16 -1.227390e-16 88.349619
std 5.212781e-01 4.822270e-01 4.036325e-01 3.300833e-01 250.120109
min -1.029540e+01 -2.604551e+00 -2.256568e+01 -1.543008e+01 0.000000
25% -3.171451e-01 -3.269839e-01 -7.083953e-02 -5.295979e-02 5.600000
50% 1.659350e-02 -5.213911e-02 1.342146e-03 1.124383e-02 22.000000
75% 3.507156e-01 2.409522e-01 9.104512e-02 7.827995e-02 77.165000
max 7.519589e+00 3.517346e+00 3.161220e+01 3.384781e+01 25691.160000
Class
count 284807.000000
mean 0.001727
std 0.041527
min 0.000000
25% 0.000000
50% 0.000000
75% 0.000000
max 1.000000
[8 rows x 31 columns]
각 열에 대한 데이터 건수, 평균, 표준편차, 최소값, q1(하위 25%), median(중앙값), q3(상위 25%), 최대값을 확인합니다.
# class 칼럼 건수 확인
creditcardData['Class'].value_counts()
----------------------------------------------------------
0 284315
1 492
Name: Class, dtype: int64
# class 칼럼 비율 확인
creditcardData['Class'].value_counts(normalize = True)
----------------------------------------------------------
0 0.998273
1 0.001727
Name: Class, dtype: float64
class 칼럼 확인 결과, 사기성 신용카드거래는 492건(0.17%)이 존재하고, 비사기성 신용카드거래는 284,315건(99.83%)이 존재합니다.
3단계: 데이터 분할
먼저, 머신러닝 분야의 대표적인 라이브러리인 sklearn에서 필요 모듈을 로드합니다. 데이터 세트를 훈련 세트와 테스트 세트로 분할하여 훈련 세트로 모델을 개발하고, 테스트 세트로 모델의 성능을 평가합니다.
# 데이터 분할을 위한 필요 모듈 로드
from sklearn.model_selection import train_test_split
# 머신러닝 학습을 위한 열 (Features) 선택
X = creditcardData.drop('Class', axis = 1)
# 머신러닝 학습을 위한 Target 변수 선택
y = creditcardData['Class']
# 데이터 분할 : 훈련 세트(80%)와 테스트 세트(20%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)4단계: 모델 훈련
훈련 데이터에 대해 머신러닝의 가장 기초적인 알고리즘인 로지스틱 회귀로 모델을 훈련합니다. 먼저, 로지스틱 회귀 모델을 학습하기 위해 필요한 모듈을 로드하는 것이 필요합니다.
# 로지스틱 회귀 모델을 훈련하기 위한 필요 모듈 로드
from sklearn.linear_model import LogisticRegression
# 로지스틱 회귀 모델 생성
logisticModel = LogisticRegression()
# 훈련 데이터에 대한 모델 적합
logisticModel.fit(X_train, y_train)
-------------------------------------------------
LogisticRegression()5단계: 모델 평가
정확도, 정밀도, 재현율, F1-Score 등 적절한 측정 항목을 사용하여 테스트 데이터를 활용하여 모델 성능을 평가합니다. 먼저, 모델 성능 평가에 필요한 모듈을 로드합니다.
# 테스트 데이터를 활용하여 예측
y_pred = logisticModel.predict(X_test)
# 모델 평가
print("Confusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred))
------------------------------------------------------------
Confusion Matrix:
[[56829 35]
[ 43 55]]
Classification Report:
precision recall f1-score support
0 1.00 1.00 1.00 56864
1 0.61 0.56 0.59 98
accuracy 1.00 56962
macro avg 0.81 0.78 0.79 56962
weighted avg 1.00 1.00 1.00 56962결과로 나오는 Confusion Matrix, Classification Report의 지표에 대한 자세한 해석은 Confusion Matrix, Precision-Recall, F1-Score 이해하기를 참고하시면 됩니다.
6단계: 시각화
신용카드 사기 거래 탐지와 같은 이진 분류 예측 문제에 대한 예측 값과 실제 값을 시각적으로 비교하기 위해 Confusion Matrix Heatmap 또는 ROC 곡선을 만들 수 있습니다.
Confusion Matrix Heatmap
# 필요 라이브러리 로드
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix
# Confusion Matrix 생성
confusionMatrix = confusion_matrix(y_test, y_pred)
# Confusion Matrix를 위한 heatmap 생성
plt.figure(figsize = (8, 6))
sns.heatmap(confusionMatrix, annot = True, fmt = "d", cmap = "Blues", cbar = False,
xticklabels = ["예측값 0", "예측값 1"],
yticklabels = ["실제값 0", "실제값 1"])
plt.xlabel('예측값')
plt.ylabel('실제값')
plt.title('Confusion Matrix')
plt.show()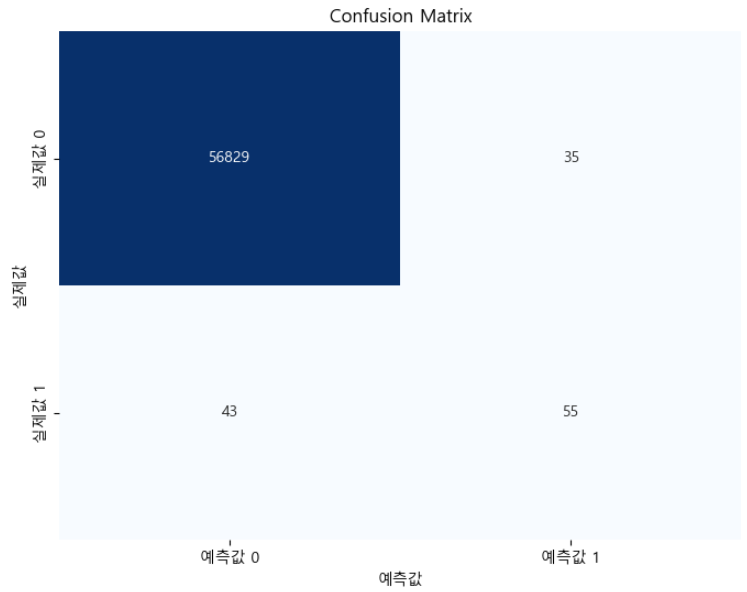
위의 코드와 산출된 Confusion Matrix Heatmap에 대한 설명은 아래와 같습니다.
- y_test는 테스트 데이터세트의 실제 값(실제 실제값)을 나타냅니다.
- y_pred는 모델의 예측 값을 나타냅니다.
이 코드는 x축이 예측 class(비사기 및 사기에 대해 각각 0과 1)를 나타내고, y축이 실제 class를 나타내는 히트맵을 생성합니다. 히트맵 셀 내부의 숫자는 각 범주에 속하는 관측치의 수를 나타냅니다.
이 시각화를 사용하면 예측 값과 실제 값을 쉽게 비교하여, 모델의 정확한 예측도와 오류 분류를 확인할 수 있습니다.
ROC curve
# 필요 라이브러리 로드
from sklearn.metrics import roc_curve, roc_auc_score, auc
# ROC 를 표시하기 위한 신용카드 사기 탐색 예측 확률값 산출
y_prob = logisticModel.predict_proba(X_test)[:, 1]
# ROC curve 계산
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
# AUROC(Area Under the ROC Curve) 계산
rocAuc = auc(fpr, tpr)
# ROC curve 출력
plt.figure(figsize = (8, 6))
plt.plot(fpr, tpr, color = 'darkorange', lw = 2, label = f'ROC curve (AUC = {rocAuc:.2f})')
plt.plot([0, 1], [0, 1], color = 'navy', lw = 2, linestyle = '--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('거짓 양성률')
plt.ylabel('참 양성률')
plt.title('ROC Curve')
plt.legend(loc = 'lower right')
plt.show()
위의 코드에 대한 설명은 아래와 같습니다.
- y_test는 테스트 데이터 세트의 실제 레이블(실제 정보)을 나타냅니다.
- y_prob는 모델에서 예측된 class 1(사기) 확률을 나타냅니다.
코드는 ROC 곡선과 AUROC(곡선 아래 면적) 점수를 계산한 다음 ROC 곡선을 그립니다. ROC 곡선은 결정 임계값을 변경함에 따라 참양성률(TPR)과 거짓양성률(FPR) 간의 균형을 보여줍니다. AUC가 높을수록 모델 성능이 더 우수함을 나타냅니다.
Precision Recall Curve
# 필요 라이브러리 로드
from sklearn.metrics import precision_recall_curve, average_precision_score
# Precision-Recall curve 계산
precision, recall, thresholds = precision_recall_curve(y_test, y_prob)
# 평균 정밀도 계산
averagePrecision = average_precision_score(y_test, y_prob)
# Precision-Recall curve 출력
plt.figure(figsize = (8, 6))
plt.plot(recall, precision, color = 'darkorange', lw = 2, label = f'Precision-Recall curve (AP = {averagePrecision:.2f})')
plt.xlabel('재현율')
plt.ylabel('정밀도')
plt.title('Precision-Recall Curve')
plt.legend(loc = 'best')
plt.show()
위의 코드에 대한 설명은 아래와 같습니다.
- y_test는 테스트 데이터 세트의 실제 레이블(실제 정보)을 나타냅니다.
- y_prob는 모델에서 예측된 clas 1(사기) 확률을 나타냅니다.
코드는 정밀도-재현율 곡선과 평균 정밀도(AP) 점수를 계산한 다음 곡선을 그립니다. 정밀도-재현율 곡선은 결정 임계값을 변경함에 따라 정밀도와 재현율 간의 균형을 보여줍니다. AP가 높을수록 모델 성능이 더 우수함을 나타냅니다.
8단계: 미세 조정 및 최적화
하이퍼파라미터를 미세 조정하고, 다양한 알고리즘(예: Random Forest, Gradient Boosting)을 시도하고, 오버샘플링 또는 언더샘플링과 같은 기술을 사용하여 class 불균형 문제를 처리하여 모델을 더욱 최적화할 수 있습니다.
성능이 좋은 모델이 있으면 실시간 사기 탐지를 위해 이를 운영 환경에 배포할 수 있습니다. 여기에는 API를 설정하거나 이를 승인 시스템에 통합하는 작업이 포함될 수 있습니다.
이상으로 신용 카드 사기 탐색 예측 모델을 산출하는 방법에 대해서 간단하게 알아 보았습니다. 다음 포스팅에서는 더 복잡한 머신러닝 기법을 활용한 모델 학습 방법에 대해서 알아 보겠습니다.
감사합니다.