이번 포스팅에서는 확률분포함수 에 대해서 알아보겠습니다. 확률분포함수 (Probability Distribution Function, PDF)는 발생 가능한 모든 결과값, 표본 공간, 그리고 주어진 범위 내에서 확률 변수가 취할 수 있는 확률값을 설명하는 함수로 최소값과 최대값 사이에 경계가 정해져 있습니다.
모든 확률분포함수는 다음 두 가지 기준을 충족해야 합니다.
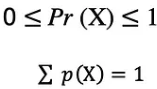
첫 번째 기준은 모든 확률이 [0,1] 범위에 속하는 숫자이고, 두 번째 기준은 모든 가능한 확률의 합이 1이어야 한다는 것입니다.
일반적으로 확률 함수는 이산 및 연속, 두 가지 범주로 분류합니다.
이산 분포 함수는 동전을 던져 두 가지 결과만 가능한 경우와 같이 셀 수 있는 표본 공간이 있는 무작위 프로세스를 설명합니다.
이산 분포 함수의 예로는 베르누이 분포 함수, 이항 분포 함수, 포아송 분포 함수, 이산 균일 분포 함수 등이 있습니다.
연속 분포 함수는 연속 표본 공간이 있는 무작위 프로세스를 설명합니다.
연속 분포 함수의 예로는 정규 분포 함수, 연속 균일 분포 함수, 코시 분포 함수 등이 있습니다.
이항분포
이항 분포는 n개의 독립적인 실험 시퀀스에서 성공 횟수의 이산 확률 분포이며, 각각은 부울 값의 결과, 즉 성공(확률 p) 또는 실패(확률 q = 1 − p)를 갖습니다.
확률 변수 X가 이항 분포를 따른다고 가정하면, n개의 독립적인 시도에서 k개의 성공을 관찰할 확률은 다음과 같은 확률 밀도 함수로 표현할 수 있습니다.
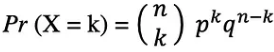
이항분포는 반복된 독립적인 실험의 결과를 분석할 때 유용하며, 특히 특정 오류율에서 특정 임계값을 충족할 확률에 관심이 있는 경우 유용합니다.
이항분포 평균과 분산은 아래와 같이 계산됩니다.
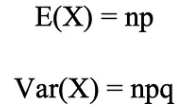
아래 그림은 이항분포의 예를 시각화한 것으로, 독립 시행 횟수가 8회이고 각 시행의 성공 확률이 16%임을 가정하고 있습니다.
# 이항 분포를 따르는 1000개의 독립적인 샘플 무작위 생성
import numpy as np
n = 8
p = 0.16
N = 1000
X = np.random.binomial(n,p,N)
# 이항분포의 히스토그램
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 20, density = True, rwidth = 0.7, color = 'purple')
plt.title("Binomial distribution with p = 0.16 n = 8")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()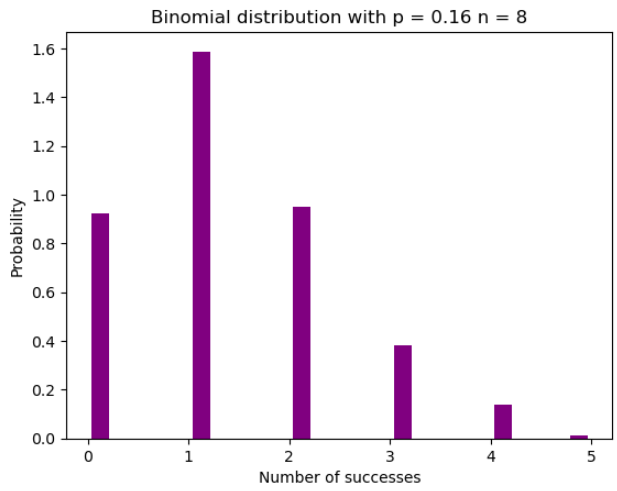
포아송분포
포아송 분포는 특정 기간 동안 발생하는 사건의 수에 대한 이산 확률 분포로, 해당 기간 동안 사건이 발생하는 평균 횟수를 고려합니다.
확률 변수 X가 포아송 분포를 따른다고 가정하면, 기간 동안 k개의 사건을 관찰할 확률은 다음 확률 함수로 표현할 수 있습니다.
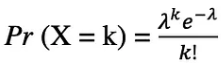
여기서 e는 Euler 수이고 λ 람다, 도착률 매개변수는 X의 기대값입니다. 포아송 분포 함수는 주어진 시간 간격 내에서 발생하는 계산 가능한 이벤트를 모델링하는 데 사용되어 매우 인기가 있습니다.
포아송분포의 평균과 분산은 아래와 같이 계산됩니다.
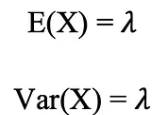
예를 들어, 포아송 분포는 오후 7시에서 10시 사이에 매장에 도착하는 고객 수 또는 오후 11시에서 12시 사이에 응급실에 도착하는 환자 수를 모델링하는 데 사용할 수 있습니다.
아래 그림은 포아송 분포의 예를 시각화한 것으로, 웹사이트에 도착한 웹 방문자 수를 세는 것으로, 도착률 람다가 7분과 같다고 가정합니다.
# 1000개의 독립적인 포아송 분포를 따르는 샘플의 무작위 생성
import numpy as np
lambda_ = 7
N = 1000
X = np.random.poisson(lambda_,N)
# 포아송 분포 히스토그램
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 50, density = True, color = 'purple')
plt.title("Randomly generating from Poisson Distribution with lambda = 7")
plt.xlabel("Number of visitors")
plt.ylabel("Probability")
plt.show()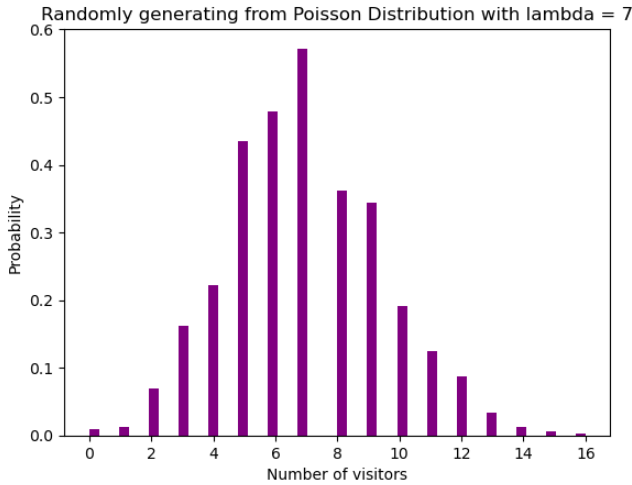
정규분포
정규분포는 실수 값의 확률 변수에 대한 연속 확률 분포로 가우시안 분포라고도 부릅니다.
사회 및 자연 과학에서 모델링 목적으로 일반적으로 사용되는 가장 인기 있는 분포 함수 중 하나입니다.
예를 들어, 사람들의 키나 시험 점수를 모델링하는 데 사용됩니다. 확률 변수 X가 정규 분포를 따른다고 가정하면 확률 밀도 함수는 다음과 같이 표현할 수 있습니다.
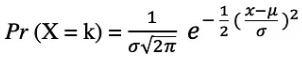
여기서 매개변수 μ(mu)는 분포의 평균으로 위치 매개변수라고도 하며, 매개변수 σ(sigma)는 분포의 표준 편차로 스케일 매개변수라고도 합니다. 숫자 π(pi)는 원주율로 원의 둘레와 지름의 비율(대략 3.14)을 의미하는 수학적 상수입니다.
정규분포의 평균 및 표준편차는 아래와 같이 표현됩니다.
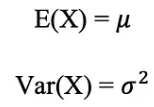
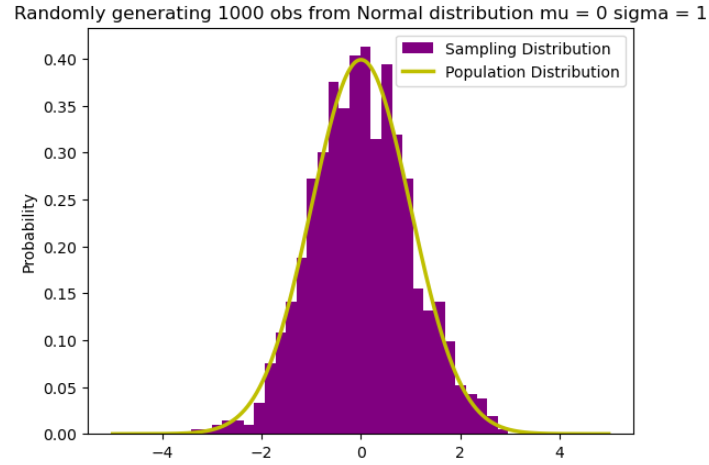
아래 그림은 평균이 0(μ = 0)이고 표준편차가 1(σ = 1)인 정규분포의 예를 시각화한 것입니다. 이를 표준정규분포라고 합니다.
# 1000개의 독립적인 정규분포를 따르는 표본의 무작위 생성
import numpy as np
mu = 0
sigma = 1
N = 1000
X = np.random.normal(mu,sigma,N)
# 모집단 분포
from scipy.stats import norm
x_values = np.arange(-5,5,0.01)
y_values = norm.pdf(x_values)
# 모집단 분포에서 추출한 표본의 히스토그램
import matplotlib.pyplot as plt
counts, bins, ignored = plt.hist(X, 30, density = True,color = 'purple',label = 'Sampling Distribution')
plt.plot(x_values,y_values, color = 'y',linewidth = 2.5,label = 'Population Distribution')
plt.title("Randomly generating 1000 obs from Normal distribution mu = 0 sigma = 1")
plt.ylabel("Probability")
plt.legend()
plt.show()