이번 포스팅에서는 통계학의 기초 개념인 확률변수 평균 분산 표준편차 에 대해서 알아보겠습니다.
영국의 수학자 칼 피어슨이 말했듯이, 통계는 과학의 문법이며 이는 특히 컴퓨터 및 정보 과학, 물리 과학, 생물 과학에 해당합니다. 데이터 과학이나 데이터 분석에서 여정을 시작할 때 통계적 지식이 있으면 데이터 통찰력을 더 잘 활용하는 데 도움이 됩니다.
“Statistics is the grammar of science.” Karl Pearson
데이터 과학 및 데이터 분석에서 통계의 중요성을 과소평가할 수 없습니다. 통계는 구조를 찾고 더 깊은 데이터 통찰력을 제공하는 도구와 방법을 제공합니다.
통계와 수학은 모두 사실을 좋아하고 추측을 싫어합니다. 이 두 가지 중요한 과목의 기본을 알면 비판적으로 생각하고 데이터를 사용하여 비즈니스 문제를 해결하고 데이터 기반 의사 결정을 내릴 때 창의적으로 행동할 수 있습니다.
사전 통계 지식이 없고, 필수적인 통계 개념을 처음부터 파악하고 배우고 싶다면, 이번 포스팅 글이 바로 여러분을 위한 것입니다. 이 글은 통계 지식을 새롭게 하고 싶은 모든 사람에게도 좋은 읽을거리가 될 것이라고 믿습니다.
확률 변수 (Random Variable)
확률 변수 (Random Variable)의 개념은 많은 통계적 개념의 초석을 형성합니다. 공식적인 수학적 정의를 이해하기 어려울 수 있지만 간단히 말해서 확률 변수는 동전 던지기나 주사위 굴리기와 같은 확률 과정의 결과를 숫자에 매핑하는 방법입니다.
예를 들어, 동전 던지기의 확률 과정을 확률 변수 X로 정의할 수 있으며, 이 확률 변수는 결과가 앞면이면 1, 뒷면이면 0의 값을 갖습니다.
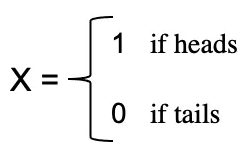
이 예에서 동전을 던지는 무작위 과정을 가지고 있으며, 이 실험은 두 가지 가능한 결과, 즉 {0, 1}을 생성할 수 있습니다.
이 모든 가능한 결과의 집합을 실험의 표본 공간이라고 합니다.
무작위 과정이 반복될 때마다 이를 사건(event)이라고 합니다. 이 예에서 동전을 던져서 결과로 앞면 혹은 뒷면이 나오는 것을 사건이라고 합니다.
이 사건이 특정 결과로 발생할 가능성을 해당 사건의 확률이라고 합니다.
사건의 확률은 확률 변수 X가 P(x)로 설명할 수 있는 특정 값 x를 취할 가능성을 의미합니다.
동전을 던지는 예에서 앞면이나 뒷면이 나올 가능성은 0.5(=50%)로 동일합니다.
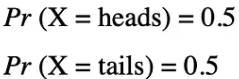
이 예에서 사건의 확률은 [0,1] 범위의 값만 가질 수 있습니다.
평균, 분산, 표준편차
평균, 분산 및 기타 여러 통계 개념을 이해하려면 모집단(Population)과 표본(Sample)의 개념을 알아야 합니다.
모집단은 우리의 관심이 되는 대상으로 모든 관찰(개인, 객체, 이벤트 또는 절차)의 집합입니다.
일반적으로 매우 크고 다양한 반면, 표본은 모집단을 대표하는 모집단의 부분 집합입니다.
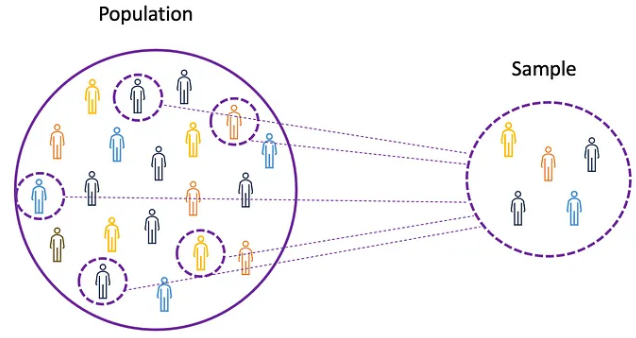
(출처: https://news.lunartech.ai/fundamentals-of-statistics-for-data-scientists-and-data-analysts-69d93a05aae7)
전체 모집단을 대상으로 실험하는 것이 불가능하거나 이에 수반되는 비용이 너무 비싸다는 점을 감안할 때, 연구자나 분석가는 실험이나 시행에서 전체 모집단이 아닌 표본을 사용합니다.
실험 결과를 신뢰할 수 있고 전체 모집단에 적용하려면 표본이 모집단을 정확하게 대표해야 합니다. 즉, 표본은 편향(bias)이 없어야 합니다.
이를 위해 임의 표본 추출(Random Sampling), 체계적 표본 추출(Systematic Sampling), 군집 표본 추출(Clustered Sampling), 가중 표본 추출(Weighted Sampling), 계층 표본 추출(Stratified Sampling)과 같은 통계적 표본 추출 기법을 사용할 수 있습니다.
평균(Mean)
평균은 유한한 숫자 집합의 중심 값입니다. 데이터의 확률 변수 X가 다음과 같은 값을 갖는다고 가정해 보겠습니다.
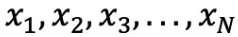
여기서 N은 모집단의 관측치 수 또는 데이터 빈도입니다. 그러면 μ로 정의된 모집단 평균은 다음과 같이 표현할 수 있습니다.
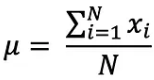
평균은 기대값이라고도 하며, 종종 E() 또는 맨 위에 막대가 있는 임의 변수로 정의됩니다. 예를 들어, 확률 변수 X와 Y의 기대값, 즉 각각 E(X)와 E(Y)는 다음과 같이 표현할 수 있습니다.
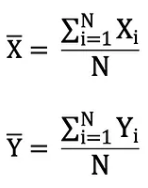
import numpy as np
x = np.array([1,3,5,6])
meanX = np.mean(x)
print("x의 평균: ", meanX)
----------------------------------------
x의 평균: 3.75분산(Variation)
분산은 관측된 데이터들이 평균값에서 얼마나 떨어져 있는지를 측정하며, 관측된 데이터 값과 평균의 차이를 제곱하여 합한 값으로 정의됩니다.
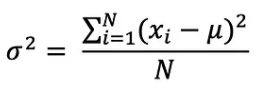
import numpy as np
x = np.array([1,3,5,6])
varianceX = np.var(x)
print("x의 분산: ", varianceX)
-----------------------------------
x의 분산: 3.6875표준편차(Standard Deviation)
표준 편차는 분산의 제곱근으로 계산되며, 시그마로 정의된 표준 편차는 다음과 같이 표현할 수 있습니다.
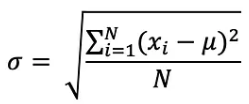
표준편차는 분산보다 더 선호되는 경우가 많습니다. 왜냐하면 관측된 데이터와 동일한 단위를 사용하기 때문에 더 쉽게 해석할 수 있기 때문입니다(예를 들어, 10명의 고등학생 키(단위: cm)를 관측한 데이터가 있다고 가정하겠습니다. 이 표본의 분산을 계산하면, 단위는 cm2 이지만, 표준편차의 계산 결과값은 cm입니다.).
import numpy as np
x = np.array([1,3,5,6])
varianceX = np.std(x)
print("x의 표준편차: ", varianceX)
--------------------------------------------
x의 표준편차: 1.920286436967152공분산(Covariance)
공분산은 두 확률 변수간의 관계를 설명합니다. 이는 두 확률 변수의 평균에서 벗어난 값을 곱한 기대값으로 정의됩니다.
두 확률 변수 X와 Z 간의 공분산은 다음 표현식으로 설명할 수 있습니다. 여기서 E(X)와 E(Z)는 각각 X와 Z의 평균을 나타냅니다.
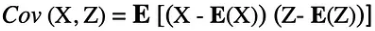
공분산은 음수 또는 양수 값과 0 값을 가질 수 있습니다. 공분산의 양수 값은 두 개의 확률 변수가 같은 방향으로 변하는 경향이 있음을 나타내는 반면, 음수 값은 이러한 변수가 반대 방향으로 변한다는 것을 나타냅니다.
마지막으로, 0 값은 함께 변하지 않는다는 것을 의미합니다.
import numpy as np
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
# 이는 대각선 요소에 대한 x_variance, y_variance 및 x, y의 공분산을 포함하는 x, y의 공분산 행렬을 반환합니다.
cov_xy = np.cov(x,y)
cov_xy
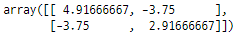
상관계수(Correlation)
상관관계는 두 변수 간의 선형 관계의 강도와 방향을 모두 측정합니다. 두 확률 변수의 값 사이에 관계 또는 패턴이 있음을 의미합니다.
두 확률 변수 X와 Z 간의 상관관계는 이 두 변수 간의 공분산을 이 변수의 표준 편차의 곱으로 나눈 것과 같으며, 이는 다음 표현식으로 설명할 수 있습니다.
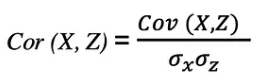
상관 계수는 -1과 1 사이의 값을 가집니다. 동일 변수의 상관 관계는 항상 1, 즉 Cor(X, X) = 1 입니다.
상관 관계를 해석할 때 명심해야 할 또 다른 사항은 상관 관계가 인과 관계가 아니라는 점입니다.
인과 관계와 혼동하지 않는 것이 중요합니다. 즉, 두 변수 사이에 상관 관계가 있더라도 한 변수가 다른 변수의 변화를 일으킨다고 결론 내릴 수 없습니다. 상관 관계는 우연일 수도 있고, 파악하지 못한 세 번째 요인이 두 변수 모두의 변화를 일으킬 수도 있습니다.
import numpy as np
x = np.array([1,3,5,6])
y = np.array([-2,-4,-5,-6])
corr = np.corrcoef(x,y)
print("x와 y의 상관관계: \n", corr)
결론
이번 포스팅에서는 통계학의 기초 개념인 확률변수, 평균, 분산, 표준편차, 공분산, 상관계수에 대해서 알아보았습니다. 다음 포스팅에서는 확률분포함수에 대해서 알아보겠습니다.